هر آنچه دربارهی دستگاههای خودپرداز میدانستید را فراموش کنید، چون نظریهپردازان رمزنگاری در حال طراحی سیستم جدیدی هستند که با اتکا به نظریهی نسبیت خاص آلبرت اینشتین به تولید دستگاههایی با امنیت بیشتر منتهی میشود.
تصور کنید صبح شنبه است و شما در راه محل کار خود از کافهای یک لیوان قهوه برای خودتان میخرید. بهمحض ورود با تابلویی مواجه میشود که اعلام میکند این کافه فقط پول نقد میپذیرد. با خود فکر میکنید مشکلی نیست و از دستگاه خودپرداز همین اطراف کمی پول نقد برمیدارم و قهوه را میخرم.
زمانی که به دستگاه میرسید، کارت بانکی خود را در شیار مخصوص دریافت کارت قرار میدهید و رمز عبور خود را وارد میکنید. در طول این فرایند ممکن است افراد دیگری که در نزدیکی شما ایستادهاند رمز شما را دیده باشند، یا ممکن است شخصی آنقدر مهارت داشته باشد که بتواند دستگاه خودپرداز را هک کند و کد شما را ذخیره کند و فکر میکنم خودتان میتوانید ادامهاش را حدس بزنید.
اینجاست که باید فکر کرد آیا یک لیوان قهوه ارزشش را داشت؟ آیا روش بهتر و امنتری وجود نداشت؟ برای پاسخ به این سؤالها، بهتر است ادامهی مطلب را بخوانید.
تیمی از محققان در کانادا و سوئیس در تلاش هستند تا برای مشکل مطرح شده راهحلی پیدا کنند. این افراد با انتشار طرح کلی خود در نشریهی Nature در اوایل ماه جاری میلادی، بهطور مفصل به توضیح ساختار دستگاه خودپرداز فوق امن خود پرداختند که قرار است این حوزه را کاملا متحول کند.
«سباستین دیزاینوله»، فیزیکدان دانشگاه ژنو که یکی از اعضای این تیم تحقیقاتی هم هست، دربارهی این طرح میگوید که فرض اطمینان به دستگاهها در زمان وارد کردن اطلاعات مربوط به احراز هویت از اساس یک مشکل است. او و محققان همکارش در این پروژه با شعار «همهی فرضها را کنار بگذارید»، قصد دارند مکانیزم دریافت پول نقد را امنتر کنند.
آنها اعلام کردهاند که این ایدهی بلندپروازانه با نظریهی نسبیت خاص فیزیکدان بزرگ، آلبرت اینشتین، ارتباط دارد و سیستم رمزگذاری در نظر گرفته شده در این طرح با روشی بهنام Zero-knowledge proof جایگزین میشود. در ادامه با شیوهی کار این سیستم جدید آشنا میشویم.
نحوهی عملکرد این سیستم اثبات Zero-knowledge چگونه است؟
آیا بازیهای فکری دوران بچگی را بهیاد دارید که برای حل کردنشان نیاز به تمرکز داشتیم؟ به بیان ساده، روش اثبات Zero-knowledge در واقع نسخهای توسعه یافته از همان بازیهای فکری است. در دانش رمزنگاری که همان مطالعهی ارتباطات امن بهشمار میآید، روشهای اثبات Zero-knowledge متدهایی هستند که با استفاده از آنها،طرف A به طرف B ثابت میکند از چیزی اطلاع دارد. نکته این است که طرف A (اثبات کننده) نمیتواند اطلاعاتی را که میداند برای طرف B (تأیید کننده) فاش کند.
راهی وجود دارد که طرف A بتواند این موضوع را حل کند؛ تصور کنید دوستی دارید که فقط میتواند سیاه و سفید ببیند، اما شما میتوانید همهچیز را رنگی ببینید. هدف شما این است که به دوست خود ثابت کنید شما میتوانید رنگهای دیگر را هم ببینید. در این صورت اگر بخواهید از روش Zero-knowledge استفاده کنید، باید به شیوهی زیر عمل کنید.
دوست شما یک کارت قرمز و یک کارت آبی پیش روی شما میگذارد. سپس کارتها را به پشت خودش میبرد که ممکن است آنها را با هم جابهجا کند یا نکند. دوباره کارتها را مقابل شما قرار میدهد و میپرسد: «آیا آنها را جابهجا کردم؟»
این کار (در واقع بازی) میتواند هزاران بار تکرار شود و شما همیشه پاسخ درست را میدهید، چون میتوانید رنگها را ببینید. بعد از چند بار تکرار این کار، دوست شما میگوید: «بسیار خب، من باور کردم. تو میتوانی رنگها را ببینی». در این موقعیت، شما با موفقیت ثابت کردهاید که توانایی تشخیص رنگها را دارید، بدون آن که رنگهایی را که میبینید فاش کنید.
دیزاینوله در توضیح روش ابداعی خودشان میگوید که روش آنها، اثبات همان مبحث سه رنگپذیری گراف است. البته مجموعهای از دانش پشت این ایده قرار دارد. سه رنگپذیری یک مسألهی پیچیدهی ریاضیاتی است که سالهاست نظریه پردازان مشغول مطالعهی آن هستند. مسألهی مورد بحث این سؤال را مطرح میکند: «چگونه میتوانید یک نقشهی بزرگ از اجسام را تنها با سهرنگ رنگآمیزی کنید، بهصورتی که هیچیک از اجسام همرنگ کنار هم قرار نگیرند؟»
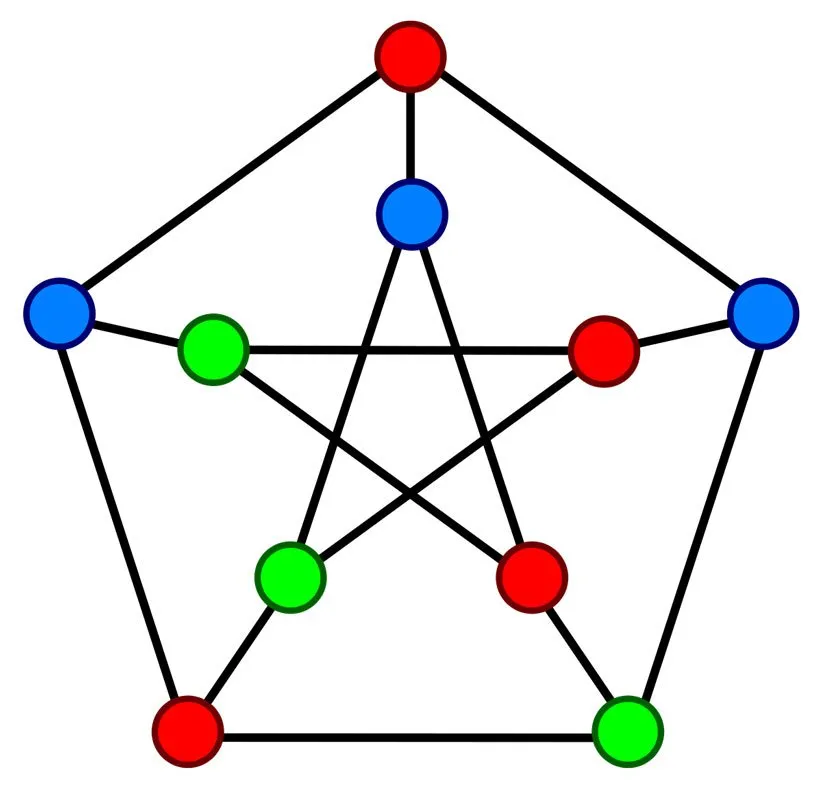
این نقشه نمیتواند شبیه نقشهی جهانی باشد که به دیدن آن عادت کردهایم. در واقع، این نقشه بهاندازهای بزرگ است که بشر برای برای درک آن به تکنولوژی متوسل شده است، اما دیزاینوله میگوید حتی با کمک گرفتن از تکنولوژی هم سالها طول میکشد تا یک راهحل پیدا کنیم.
او با انتقال همین مفهوم به دنیای خودپردازها، این ایده را مطرح میکند که به هر فرد یک نقشهی رنگآمیزی شدهی منحصربهفرد با یک راه حل سه رنگپذیری از قبل برنامهریزی شده داده شود. برای دریافت پول از دستگاه، هر فرد باید دستگاه را به یک خروجی اکسترنال روی خودپرداز وصل کند که این دستگاه اکسترنال همان اثبات کننده و خودپرداز همان تأیید کننده است.
دستگاه خودپرداز با طرح هزاران سؤال مرتبط با بخشهای رنگی نقشهی شما، به جستوجوی دستگاهی که به آن متصل کردهاید میپردازد. با وجود پیچیدگی مبحث سه رنگپذیری، دستگاه شما فوری به سؤالات پاسخ میدهد چون از قبل برنامهریزی شده است.
علاوه بر این، بهدلیل اینکه هر بار سؤالها بهصورت تصادفی انتخاب میشوند، حتی اگر تأیید کننده دربارهی زوایای مختلف بپرسد، خودپرداز هیچگاه اطلاعات کافی برای دانستن تمام نقشه را دریافت نخواهد کرد که به گفتهی دیزاینوله این یک نکتهی حیاتی است.
مانند همان شرایط دوستمان که فقط سیاه و سفید را میدید، خودپرداز هم شما را تأیید هویت میکند و پول را به شما تحویل میدهد، چون دستگاه شما پشتسر هم به سؤالها پاسخ صحیح میدهد. در نهایت خودپرداز هم مانند آن دوستمان، صداقت ما را باور میکند.
بهیاد داشته باشید، همهی پیشفرضها را کنار بگذارید
سیستم ابداع شده برای خودپردازها قابل اطمینان بهنظر میرسد. اما دیزاینوله و تیمش معتقدند که باید همهی پیشفرضها را کنار بگذاریم. آنها هنوز بهصورت کامل به امن بودن سیستم نقشهی سهرنگ اعتماد ندارند. در واقع آنها بر سر این موضوع بحث دارند که ممکن است شخصی پاسخهای پراکندهی دستگاه دربارهی نقشهاش را ضبط کند و سعی کند با محاسبهی معکوس تصویر کامل نقشه، جعل هویت کند.
این محقق سوئیسی میگوید: «این عملکردهایی که در یک جهت انجام میدهید، بسیار دشوار هستند، اما پردازش آنها در جهت دیگر غیر ممکن نیست».
برای مثال، اگر شما دو عدد اول را ضرب کنید و یک عدد بسیار بزرگ داشته باشید، سخت است که بتوانید به اعداد تک رقمی برگردید. اما این دشواری مانع انجام کار نمیشود. همین موضوع دربارهی سه رنگپذیری هم صادق است.
پس چگونه میتوانیم این مکانیزمها را به یک سطح امنیتی مطلق برسانیم؟ دیزاینوله برای پاسخ به این پرسش، به کمک خواستن از هر دو دستگاه اشاره میکند:
ایدهی پشت این سیستم دقیقا همان ترفندی است که یک پلیس در هنگام بازجویی از دو متهم جدا در دو اتاق جداگانه از آن بهره میگیرد تا دو متهم نتوانند با یکدیگر ارتباط برقرار کنند. اگر هر دوی آنها نسخهای یکسان از داستان را تعریف کنند، این میتواند نکتهای باشد که راستگویی آنها را اثبات کند.
به دستگاه خودپرداز برگردیم؛ با دو دستگاه، شما در واقع خود را به دو اثبات کننده تقسیم میکنید، مانند دو متهم مثال بالا. سپس، دو تأیید کننده بهصورت همزمان از اثبات کنندهی مربوطهی خود سؤالات معمول سه رنگپذیری را میپرسند.
بله، درست متوجه شدهاید. در این روش شما باید دو دستگاه جداگانه را به دو خودپرداز جداگانه وصل کنید! در حال حاضر، نتیجهی کار این محققان با خودپردازهایی با فاصلهی ۶۰ متر از هم کار میکند. اما آنها میگویند که میتوان این فاصله را به یک متر هم رساند. این طرح بسیار عذابآور بهنظر میرسد، اما باید بهیاد داشته باشیم که هدف این آزمایشها این است که بتوان یک مکانیزم امن را برای دستگاههای خودپرداز شبیهسازی کرد. این طرح، حداقل در حال حاضر، در حد تئوری است.

اگر هر یک از اثبات کنندهها دانش غیر محاسباتی یکسانی داشته باشند، میتوان با اطمینان گفت که احراز هویت بهدرستی انجام شده است. مانند مثال دو متهم در بازجوییهای جداگانه، دو دستگاه اثبات کننده هم نمیتوانند با یکدیگر ارتباط داشته باشند. هر هکر احتمالی که بخواهد به این سیستم نفوذ کند، باید ۲ محاسبهی معکوس از نقشههای پیچیده را بهصورت همزمان انجام دهد که اگر نگوییم امری غیر ممکن است، باید گفت یک چالش استثنائی است.
شاید با خود بپرسید که همهی این داستانها و توضیحات به نظریهی نسبیت خاص اینشتین چه ارتباطی دارند؟ دقیقا در این مرحله است که آقای فیزیکدان وارد بحث ما میشود. دلیل این که دو دستگاه اثبات کننده نمیتوانند با یکدیگر ارتباط داشته باشند، این است که بهوسیلهی نظریهی نسبیت خاص محدود شدهاند.
ما نمیتوانیم سریعتر از سرعت نور سفر کنیم
نظریهی نسبیت خاص اینشتین بهزیبایی قلمروهای فضا و زمان را بههم پیوند میدهد. اما چیزی که برای تیم سوئیسی مهم است، این است که این نظریه سرعت جابهجایی اطلاعات را هم محدود میکند.
محقق سوئیسی میگوید که با توجه به نسبیت خاص، کاملا منطقی بهنظر میرسد که این فرض کامپیوتری -و نه فیزیکی- را باور داشته باشیم که اطلاعات نمیتوانند سریعتر از سرعت نور جابهجا شوند. تا زمانی که دو خودپرداز سوالات مخصوص خود را بهقدری سریع از دستگاههای متصل شدهی حاوی نقشه بپرسند که تأخیر همیشه کمتر از زمان لازم برای انتقال اطلاعات باقی بماند (با سرعت نور محدود شود)، ما احتمال ارتباط دو دستگاه با یکدیگر را رد میکنیم.
به بیان سادهتر، در این شرایط اثبات کنندهها نمیتوانند با همدستان خود ارتباط برقرار کنند تا هویت یک کاربر را جعل کنند. در نهایت، تنها یک مسأله باقی میماند. زمانی که وارد بحث فیزیک غیر کلاسیک (نوین) و رایانش کوانتوم میشویم، این محدودیتهای نسبیتی چندان سفتو سخت نیستند.
روزنههای کوانتومی و خروج از جهان فرضی

نور در دنیای کوانتومی عملکرد متفاوتی دارد. مکانیزمهای کوانتومی اصلی شگفتانگیز بهنام «برخورد کوانتومی» را ممکن میکنند که در توضیح آن بهزبان ساده باید گفت، هنگامی که دو ذرهی کوانتومی-برای مثال ذرات نور- با هم برخورد میکنند، میتوانند بهصورت آنی با هم ارتباط برقرار کنند.
در این شرایط حتی بحث سرعت انتقال اطلاعات هم مطرح نیست. همهچیز بیدرنگ اتفاق میافتد. اگر ذرهی A دانشی از چیزی داشته باشد، میتوان کاملا مطمئن بود که ذرهی B هم اکنون از آن مطلع است.
دیزاینوله با اشاره به هکرهای احتمالی این سیستم میگوید که فرض کنیم من گراف رنگی را نداشته باشم، اما تظاهر کنم که آن را دارم، میتوانم با استفاده از برخورد کوانتومی بین دو چیپ به روشی دست پیدا کنم که به جواب صحیح برسم. در واقع، میتوانم تقلب کنم.
در حالی که او و تیمش باور دارند که مکانیزم توسعه یافته توسط آنها باید بتواند در مقابل هکرهای کوانتومی محافظت ایجاد کند، نمیتوانند ۱۰۰ درصد اطمینان دهند که چنین چیزی ممکن است. با این حال، آنها فعلا در حال بررسی پروتکلی هستند که بتواند بهجای دستگاههای اثبات کنندهی استاندارد فعلی، از اثبات کنندههای کوانتومی استفاده کند.
اگر تا اینجای ماجرا را متوجه شدید و حوصلهاتان سر نرفته، ممکن است به این فکر کنید که این خودپردازهای فوق امن از لحاظ نظری دقیقا چگونه هستند و آیا ممکن است روزی به واقعیت تبدیل شوند؟
محققان این پروژه میگویند که در حال حاضر، مسألهی اصلی برای آنها هزینه است. برای ساخت چنین دستگاههایی به مکانیزمی نیاز است که چیپهای آن با چیپهایی که روی کارتهای بانکی امروزی یافت میشود متفاوت باشند. این چیپها باید بسیار قدرتمند باشند که همین عامل باعث افزایش قیمت آنها خواهد شد.
یک ایده برای تولید این چیپها این است که سیستم طراحی شده توسط محققان در اختیار شرکتهای بزرگی که اطلاعات امن را مبادله میکنند و میتوانند از پس چنین هزینهای بربیایند قرار بگیرد.
این ایده محدودیتهای نسبیتی را کمی سبکتر میکند، چون فاصلهی بین هر دستگاه و خودپرداز تأیید کننده بیشتر خواهد شد و در نتیجه، نور هم برای انتقال بین دو طرف ارتباط به زمان بیشتری نیاز دارد. این یعنی فضای بیشتری برای تأخیرها وجود خواهد داشت، پیش از این که هکرها بتوانند به سیستم نفوذ کنند.
جدا از کاربردهای واقعگرایانه این سیستم، سباستین دیزاینوله میگوید از نظر خودش، این که ببیند حل یک مشکل ساده میتواند تا این حد سخت باشد بسیار جالب است.